
户儿
古希腊数学家毕达哥拉斯曾说过「万物皆数学」,他认为数学是构成宇宙的基础。如果你留心观察就会发现,不仅我们的生活处处离不开数学,就连昆虫世界也充满数学奥秘。
昆 虫 与 质 数
周期蝉

来源:en.wikipedia.org
晚秀蝉 Magicicada septendecim
美国著名的周期蝉(秀蝉属Magicicada )俗称魔法蝉,其若虫的蛰伏周期长达13年或17年,因而也被称为13年蝉或17年蝉。
也许大家会有疑问,周期蝉为何会设定13或17这样特别的数字作为自己的生命周期?

来源:wikipedia
要想弄明白这个问题,我们首先要清楚13和17是什么样的数字。
对数字比较敏感的小伙伴估计就能立马想到,13和17都是质数。在数学上,这两个质数代表除了1和它本身以外不能被其他数整除。
而在自然界,有研究学者猜测这两个质数生命周期可能意味着周期蝉与其他同类及天敌相遇的概率大大降低。

来源:Ken Childs
一种观点认为,周期性蝉是从非周期性蝉进化而来的,合数生命周期的蝉频繁的相遇,而产生激烈的种内竞争。而质数生命周期的蝉在最少的相遇机会下相安无事,实现种群的存续。
比如,13年蝉和17年蝉, 每221年才会同时出现一次,这样就最大限度地避免了争抢食物的“搏杀”。

来源:ento.psu.edu
另一种假设认为,周期蝉选择质数作为生长周期,巧妙地避开捕食者“有针对性”的生长周期。蝉遇到的天敌的生命周期如果是蝉生命周期的因子,那么蝉被捕食的几率就会大幅提高。
比如如果选择12年为周期,那么蝉就会和1年繁殖一代、2年繁殖一代、3繁殖一代、4繁殖一代、6年繁殖一代以及12年繁殖一代的天敌重叠, 被吃掉的可能性就要大增。

而13年蝉和17年蝉,都是质数蝉,可以幸运地避开这种遭遇天敌的可能性。

来源:www.ajc.com
当然,从遗传的角度也可以解释为什么周期蝉的生命周期是13和17两种质数。如果是合数的周期,比如说16年蝉,它的生命周期可能和1年蝉、2年蝉、4年蝉、8年蝉相遇重合, 这样它的基因可能因杂交被反复“冲淡”,从而影响后代的稳定性。
如果是13年蝉,那么它的生命周期将只和1年蝉相遇重合,基因被冲淡的可能性大大降低。

来源:www.pbslearningmedia.org
昆 虫 与 几 何
蜜蜂

来源:calculate.org.au
蜜蜂的蜂巢是严格的六角柱形体。它的一端是六角形开口,另一端则是封闭的六角棱锥体的底,由三个相同的菱形组成。蜂巢组成底盘的菱形的所有钝角都是109°28′,所有的锐角都是70°32′。
如果要消耗最少的材料,制成最大的菱形容器正是这个角度。从这个意义上说,蜜蜂称得上是"天才的数学家兼设计师"。

© Waugsberg
蝶卵
蝶卵形态变化多端,许多种类表面常呈现几何图案的刻纹及种种突起。
六边形:

来源:wewanttolearn.wordpress.com
珀灰蝶马来亚种 Pratapa deva relata

来源:wewanttolearn.wordpress.com
三尾紫灰蝶 Arhopala abseus
其他形状:
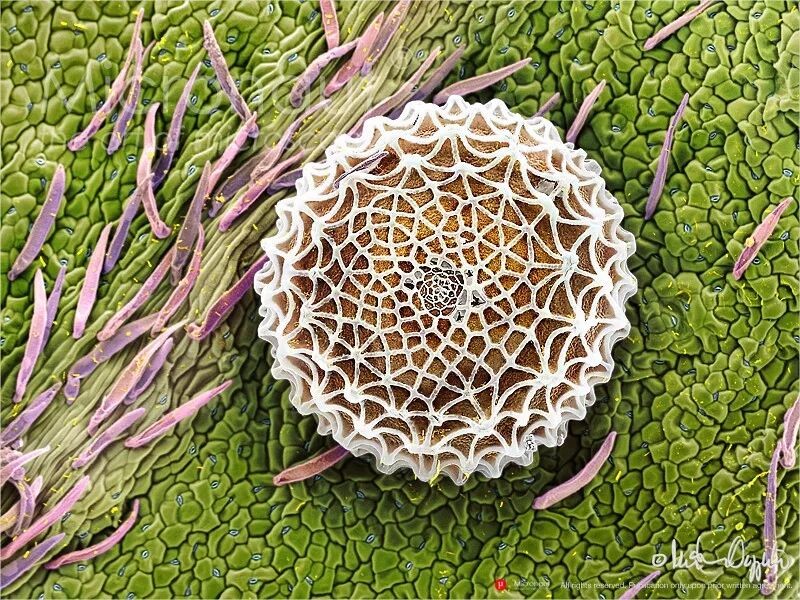
Photograph by Martin Oeggerli
阿多尼斯蓝蝶的卵扁平盘状,卵壳表面是纵横交错的网纹结构。表面凹凸不平的卵壳能够最大限度地保护卵的安全。

来源:www.photomacrography.net
宝绿灰蝶的卵精巧可爱,模样就像是从高空鸟瞰的大型体育场馆。
昆 虫 与斐 波 那 契螺 旋 线
斐波那契螺旋线,也称“黄金螺旋”,是根据斐波那契数列画出来的螺旋曲线。
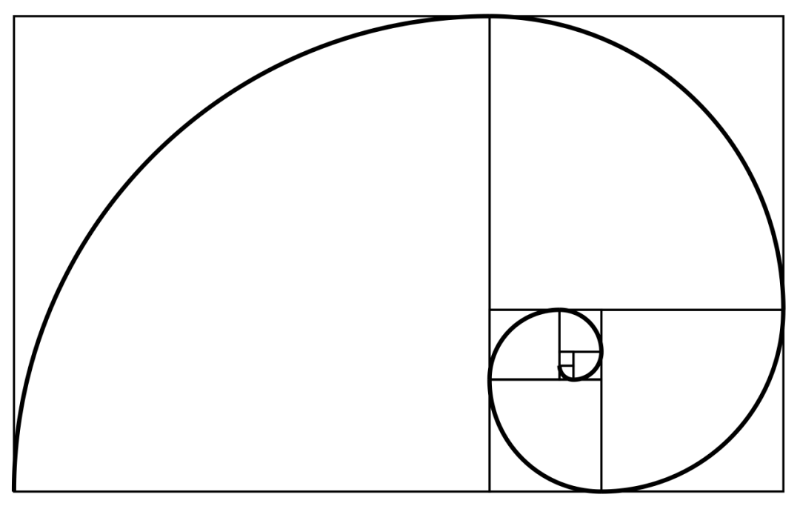
来源:commons.wikimedia.org
自然界中存在许多斐波那契螺旋线的图案,比如层叠生长的多叶芦荟,它的叶子紧密地按照螺旋结构生长。

来源:darkroastedblend
多叶芦荟
而昆虫中也存在斐波那契螺旋线,例如飞蛾的飞行轨迹:
飞蛾在夜间有一种特殊的导航方式:横向定向。即它会与月亮(光源)保持一定的角度飞行,从而能够保持直线的飞行路径,但是,这种方式只在光源离飞蛾较远的情况下才有效。
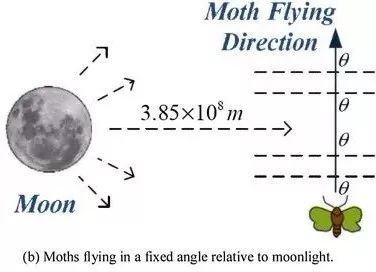
© Al-Attar AliMohamed et al
当有人造光源存在时,飞蛾会被人工灯光所欺骗,一直保持与人造灯光相同的角度飞行,由于它与光源的距离过近,它飞行的路径已经不是直线,而是一种螺旋的路径。
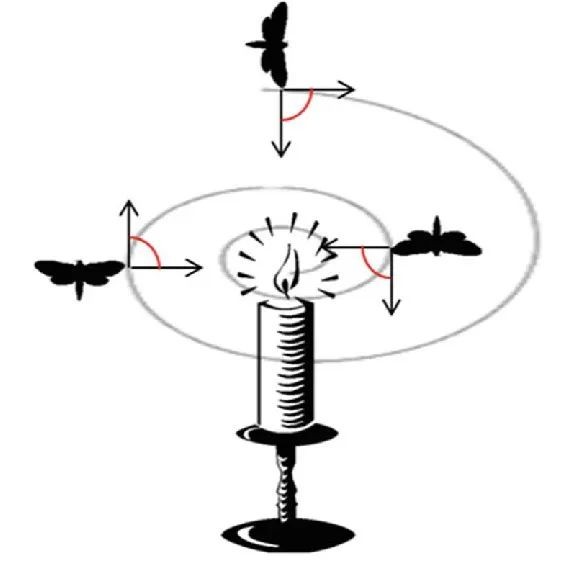
来源:www.researchgate.net
蜂类的巢穴结构:

来源:www.smithsonianmag.com
黑类四无刺蜂 Tetragonula carbonaria
蝶卵的精巧构造:

来源:wewanttolearn.wordpress.com
美姬灰蝶锡金亚种 Megisba malaya sikkima
看到这里,只能说昆虫的智慧远远超出我们的想象。